Zenone di Elea non voleva creare semplici rompicapi, ma difendere la filosofia del maestro Parmenide. L'obiettivo dei suoi paradossi era dimostrare che il concetto di movimento, che noi percepiamo con i sensi, è in realtà logicamente contraddittorio e impossibile. Se il movimento porta a conclusioni assurde, allora deve essere un'illusione (Doxa) e la vera realtà è immobile, come sostiene la ragione (Logos).
I quattro paradossi contro il movimento
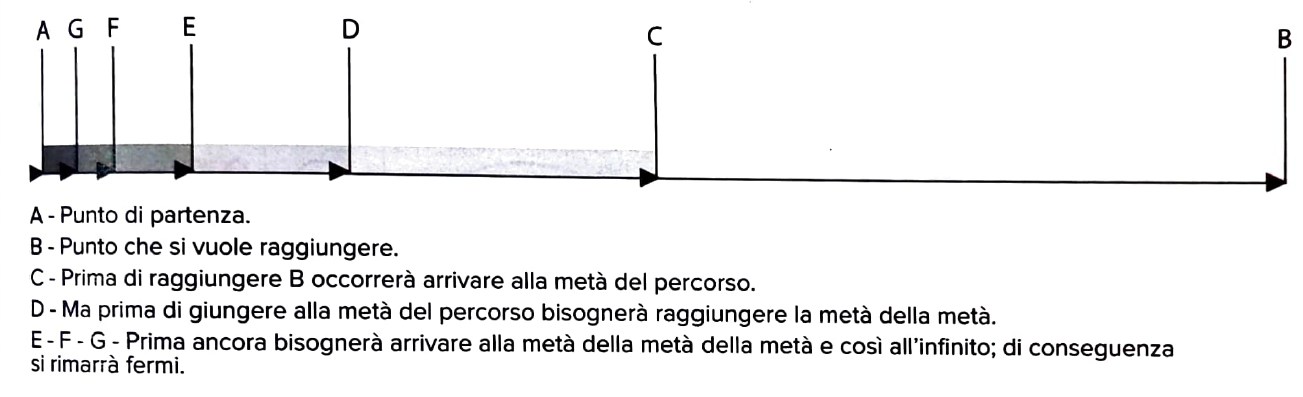
1. Il paradosso dello stadio (o della dicotomia)
Questo paradosso dimostra che il movimento non può nemmeno iniziare.
L'argomento. Immagina un corridore che voglia percorrere una distanza. Per arrivare alla fine, deve prima raggiungere la metà del percorso. Ma prima di raggiungere la metà, deve percorrere la metà di quella metà (un quarto del totale). E prima ancora, la metà di un ottavo, e così via, all'infinito.
La conclusione: Poiché lo spazio è infinitamente divisibile, il corridore dovrebbe compiere un numero infinito di spostamenti in un tempo finito. Visto che è impossibile completare un'infinità di compiti, il corridore non potrà mai nemmeno partire.
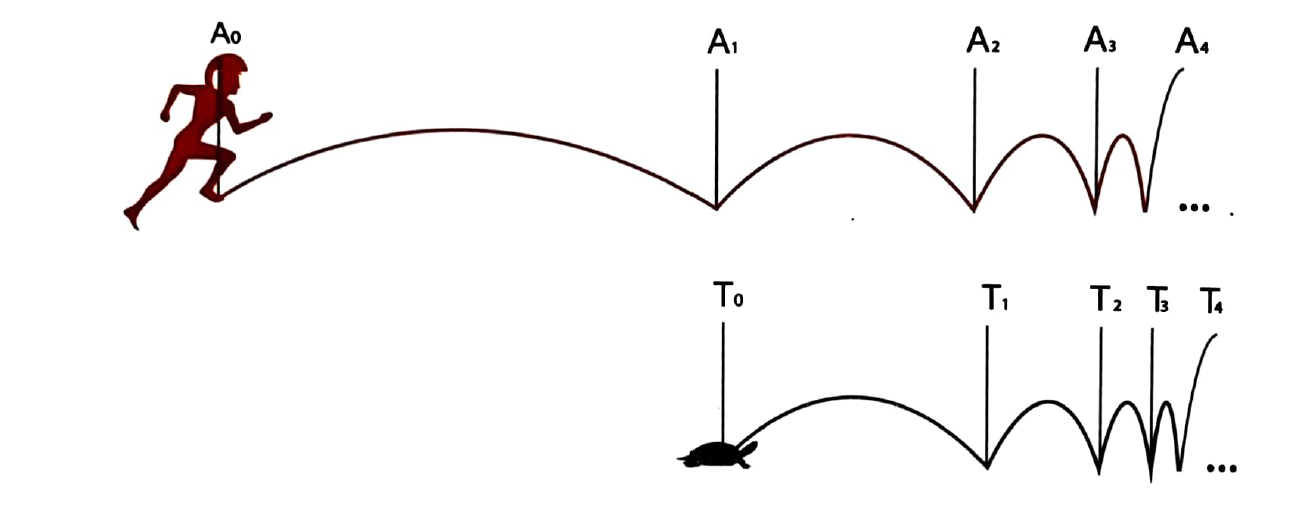
2. Il paradosso di Achille e la tartaruga
Questo è il paradosso più celebre di Zenone e dimostra che il più veloce non potrà mai raggiungere il più lento.
L'argomento: Achille, il "piè veloce", gareggia con una lenta tartaruga, concedendole un vantaggio iniziale. Per raggiungere la tartaruga, Achille deve prima arrivare al punto da cui essa è partita. Nel tempo che impiega, però, la tartaruga si è spostata un po' più avanti. Achille deve quindi raggiungere questa nuova posizione, ma nel frattempo la tartaruga si è spostata ancora. Questo processo si ripete all'infinito.
La conclusione: la distanza tra i due diventerà sempre più piccola, ma logicamente esisterà sempre. Achille non raggiungerà mai la tartaruga.
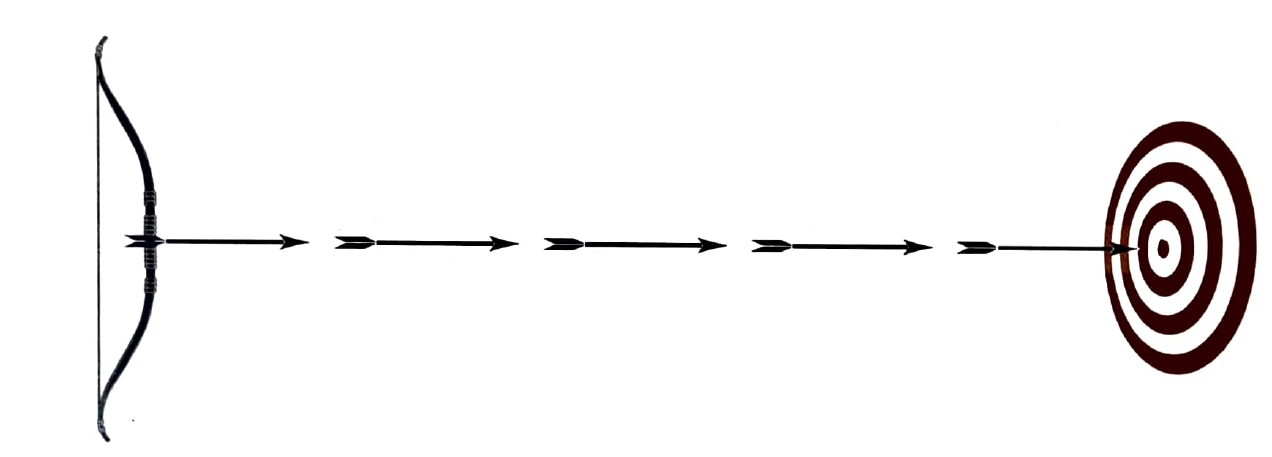
3. Il paradosso della freccia
Questo paradosso sostiene che un oggetto in movimento è, in realtà, sempre fermo.
L'argomento: consideriamo una freccia in volo. Se analizziamo il suo percorso, possiamo scomporre il tempo in una serie di singoli istanti. In un dato istante, che non ha durata, la freccia occupa una posizione precisa dello spazio, uguale alla sua lunghezza. In quell'istante, la freccia non si sta muovendo: semplicemente, è lì. È ferma.
La conclusione: se la freccia è ferma in ogni singolo istante del suo volo, e il volo non è altro che la somma di questi istanti, allora la freccia è sempre ferma. Il movimento è un'illusione.
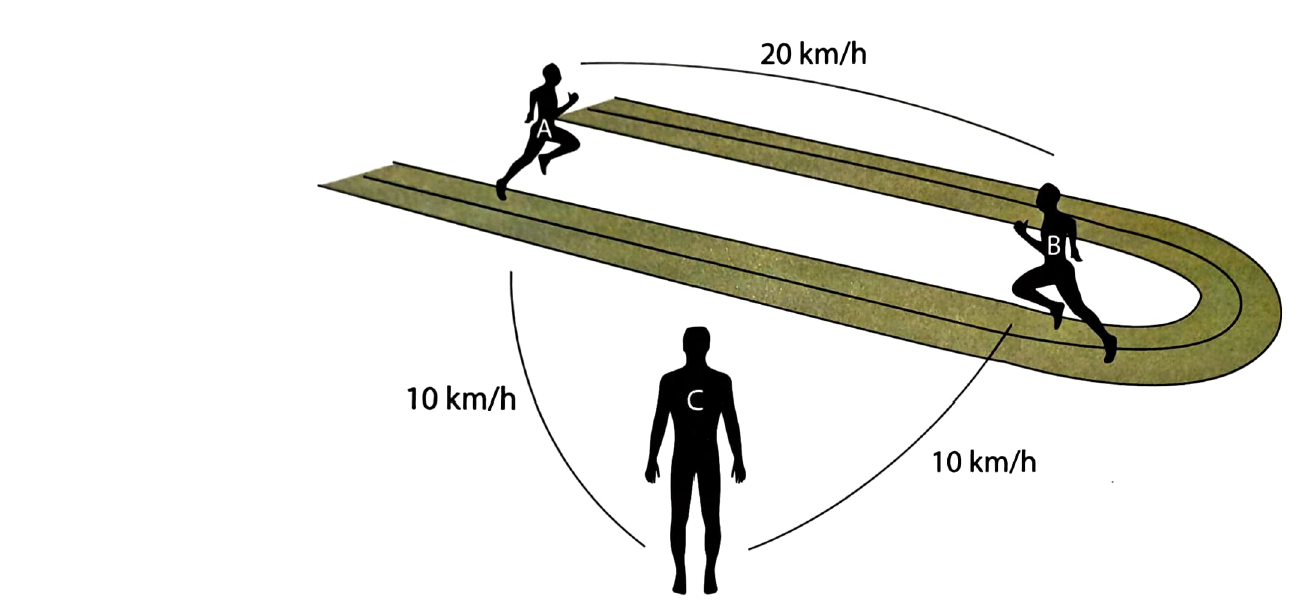
4. Il paradosso dello stadio (o delle masse in movimento)
Questo paradosso attacca l'idea che lo spazio e il tempo siano composti da unità minime e indivisibili (atomi di tempo e spazio).
L'argomento: immaginiamo tre file di corpi (A, B, C) in uno stadio. La fila C è ferma. Le file A e B si muovono a velocità identica ma in direzioni opposte. Dopo un singolo istante indivisibile, la fila B si è mossa di una posizione rispetto alla fila C (ferma), ma di due posizioni rispetto alla fila A (che le veniva incontro).
La conclusione: questo porta a una contraddizione. Per percorrere metà della distanza rispetto ad A (una posizione), B avrebbe dovuto impiegare metà tempo. Ma questo è impossibile, perché abbiamo ipotizzato che l'istante di tempo fosse indivisibile. Pertanto, l'idea stessa di movimento in un tempo "atomico" è assurda.
L'eredità dei paradossi
Sebbene la matematica e la fisica moderne abbiano fornito risposte a queste sfide (ad esempio con il calcolo infinitesimale), il valore filosofico dei paradossi di Zenone rimane immenso. Essi ci costringono a mettere in discussione la natura profonda dello spazio, del tempo e dell'infinito, mostrando l'enorme divario tra la percezione intuitiva e la coerenza logica.